Diffrentiation and integration
On the Sunday morning, I'd like make new post about Integral and diffrentiation
Calculus – differentiation, integration etc. – is easier than you think. Here's a simple example: the bucket at right integrates the flow from the tap over time. The flow is the time derivative of the water in the bucket. The basic ideas are not more difficult than that. Calculus analyses things that change, and physics is much concerned with changes. For physics, you'll need at least some of the simplest and most important concepts from calculus. Fortunately, one can do a lot of introductory physics with just a few of the basic techniques.
So stick with us: differentiation really is just subtracting and dividing, and integration really is just multiplying and adding. This short introduction is no substitute, however, for a good high school calculus course: we shall take some short cuts of which mathematicians may disapprove.
Calculus – differentiation, integration etc. – is easier than you think. Here's a simple example: the bucket at right integrates the flow from the tap over time. The flow is the time derivative of the water in the bucket. The basic ideas are not more difficult than that. Calculus analyses things that change, and physics is much concerned with changes. For physics, you'll need at least some of the simplest and most important concepts from calculus. Fortunately, one can do a lot of introductory physics with just a few of the basic techniques.
So stick with us: differentiation really is just subtracting and dividing, and integration really is just multiplying and adding. This short introduction is no substitute, however, for a good high school calculus course: we shall take some short cuts of which mathematicians may disapprove.
Differentiation: How rapidly does something change?
- The velocity is the rate of change of displacement. Let's look at a
very simple case. The strange man in this animation is moving in a
straight line at a constant speed of one metre per second. This means
that, for each second he travels, his displacement from the starting
position increases by 1 m.
(An aside for physicists: velocity is a vector, meaning that it has direction as well as magnitude. So here we could say that his speed is 1 m/s but his velocity is 1 m/s towards the right. In these examples, we shall consider only motion in a straight line, so we can specify the direction simply thus: Positive velocity means going to the right, negative velocity means going to the left. By the way, the magnitude of velocity is called the speed, which we could write as |v|. Speed is a scalar, velocity is a vector. See vectors to revise.)
When the clock strikes zero, he is at x = 3 m. We call this his initial displacement and write x0 = 3 m.
When the clock reads t = 2 s, he is at x = 5 m. So what is v? Displacement has increased by 2 m, time has increased by 2 s, so v is
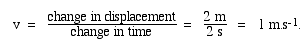
 , pronounced 'v bar'.
, pronounced 'v bar'.
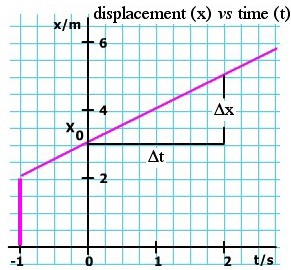
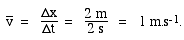  are the same. The derivative of x in this case is constant, as we show in the v(t) graph above. are the same. The derivative of x in this case is constant, as we show in the v(t) graph above.
|
Varying derivatives
-
What if v is not constant? Here's a simple case in which the same bloke
is accelerating forwards, so his velocity is increasing. Let's work out
his velocity at any particular time t, just from the graph x(t). We want
to find the slope of this curve, at different values of t, as is shown
in the animation. How can we do it? Well, in most cases, and especially
in the case of experimental measurement, we do the same thing that we
did for the simple case: we draw a triangle and put change in
displacement Δx over change in time Δt. Again, this is numerical
differentiation.
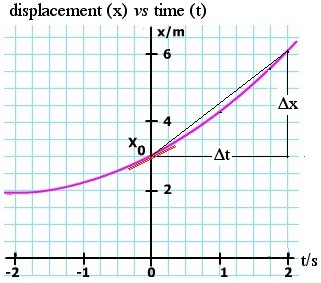
We can do better by taking a smaller value of Δt. At first, we expect the estimate to improve as we take smaller and smaller Δt. Here arises a practical problem: If we are measuring the values, there is inevitably a limit to the precision of each measurement and, as the Δt and Δx get smaller, this error becomes proportionately more important. If we are calculating x and t numerically, we face the same problem. So, in practice, we make a compromise on the size of Δt: small enough to give the local shape of the curve but large enough that the measurement or calculation errors are small. There are other tricks that we'll see below. |
Analytical derivatives
-
But what if we 'know' the formula for the function x(t)? I have put
'know' in quotation marks, because for anything in physics, the only
things that we know are the measurements. There are only a finite number
of these, so we just have a set of points on a graph. What we can do is
to find a mathematical model, a formula that goes close to the points
on the graph. For example, if the acceleration is constant, we might use
x = x0 + v0t + ½at2, as we do in the chapter on constant acceleration.
We can now choose whatever t we like, and calculate x to whatever
precision we need, though of course the final precision will depend on
how well we know x0, v0 and a, so we are still limited by measurement.
Power terms and polynomials
-
Let's have a look at these terms in turn. If x = x0, then it's simple: no variation in x, so the derivative would be zero. What about x = v0t, in other words constant velocity? This is like the first example we did: the derivative is constant, and it equals v0.
So, the derivative of a constant is zero, and the derivative of a term
that is proportional to t is just the constant of proportionality or, in
standard terms, the coefficient of t.
But what of a term like x = Ct2? (In our example, C =
a/2, but let's keep it general.) Let's make the 'run' for our slope
calculation from t to (t+Δt). Then the 'rise' on the triangle will be
from Ct2 to C(t+Δt)2. So the slope is
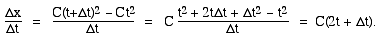
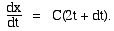
-
At this stage, if you were doing this in a mathematics school, you might
start to worry about infinitesimals, and taking the limit as Δt goes to
zero. I may get into trouble for pointing this out, but the universe
doesn't have infinitesimals, and quantities don't go to zero in physics.
Infinitesimals, like many things in mathematics, are human inventions.
So, for most purposes in physics, the limit taken is just the size
necessary to have mathematical precision greater than that of our
measurements, or greater than that of our numerical calculation. (You
really should take that mathematics course, but you won't need
infinitesimals in physics.)
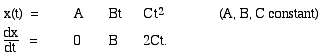
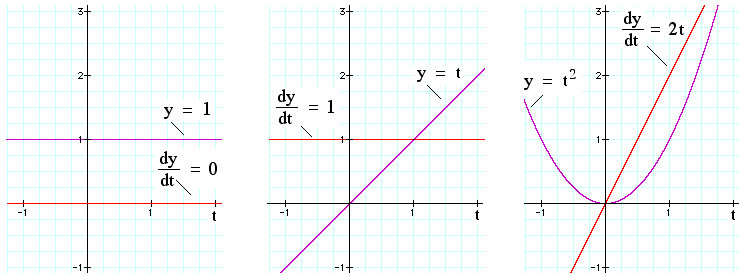
Perhaps you see a pattern here? Taking a positive integer n, and expanding (t + Δt)n, you'll see that, if y = Ctn, the derivative of y is nCtn−1. This is often written thus:
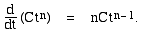
Sums of terms
-
If x is increasing with rate (dx/dt) and y is increasing with rate
(dy/dt), what is the rate of increase in (x+y)? This is an easy one: if,
over a certain time t+ Δt, x increases by Δx and y increases by Δy,
then the change in (x+y) is (Δx+Δy).
The rate of change in the sum of functions is equal to the sum of their
individual rates of change. (The derivative of the sum is the sum of the
derivatives.) With this unsurprising result, we can now differentiate
polynomials, such as this: If
- y = A + Bt + Ct2 Dt3, then
dy/dt = B + 2Ct + 3Dt2.
Trigonometric functions
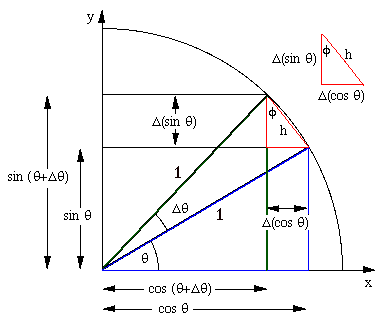
In this diagram, first look at the triangle with blue sides. The radius is drawn at the angle θ. The vertical side is, by definition, sin θ and the horizontal side is cos θ. Now let's change θ by an amount Δθ: we get another radius and another triangle, shown here with two of its sides in green. By how much have we changed sin θ? In other words, what is Δ(sin θ)? By definition, Δ(sin θ) is the amount that in θ increases when θ increases by Δθ). So it must be (sin(θ+Δθ) − sin θ). On this diagram, Δ(sin θ) is shown as the rise of the small triangle, shown in red. (For clarity, this triangle is repeated outside the main diagram.) The run of this triangle is −Δ(cos θ). The run goes to the left in this case, so it has a negative sign. This negative sign arises because, as θ increases in this quadrant, cos θ decreases. Now look at the small right triangle in red. We call its hypotenuse h. Applying the definition of sine and cos, and remembering that the cos θ is decreasing, we have
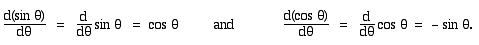 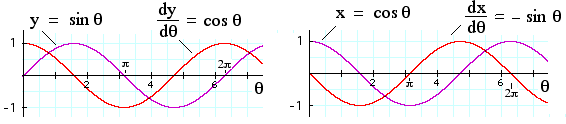 * Note the use of the definition: angle in radians = arc/radius.
Consequently, the dθ in these equations must be expressed in radians. To
convert degrees into radians, multiply by π and divide by 180°.
* Note the use of the definition: angle in radians = arc/radius.
Consequently, the dθ in these equations must be expressed in radians. To
convert degrees into radians, multiply by π and divide by 180°.
|
The chain rule
-
Suppose we have a function z that depends on t, in a way that allows us
to calculate z if we know t. And suppose that x depends on z in a
similarly explicit way. Just by cancelling a factor, we can write:
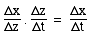
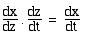
Circular and Simple Harmonic Motion
-
In both these cases, we consider uniform circular motion, in which the
angle θ increases linearly with time, so (dθ/dt) is a constant, called
the angular velocity ω. We can write this as
-
θ = ωt + φ
-
y = A.sin θ = A.sin (ωt + φ),
-
vy = dy/dt = (dy/dθ).(dθ/dt) = (A.cos θ).(ω) = A.ω.cos (ωt + φ).
Integration: How do the results of a variable rate add up?
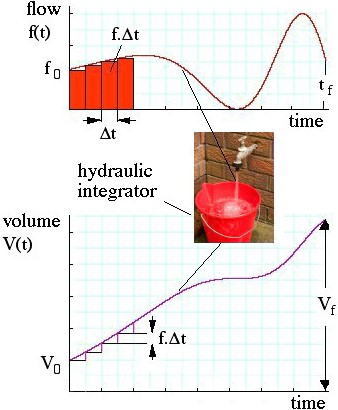
Similarly, at any time later, the volume going into the bucket in the short interval Δt is approximately f.Δt. So, for each Δt we add a step of f.Δt to the height of the purple curve representing the volume in the bucket, as shown in the lower curve. Notice that, when the flow is high, the area f.Δt is large, so that is when the volume in the bucket increases rapidly. Note that, when the flow falls to zero (tap off), the volume is no longer increasing. And of course a fall in the V(t) curve would mean water flowing out of the bucket, which we should call negative flow into the bucket. (For example, the bucket might have a leak.) What is the volume Vf in the bucket at a final time tf? (The subscript f here stands for 'final', not flow.) We can find the approximate volume as
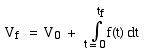 Perhaps now is a good time to go back to the animations above and check that integrating the velocity (finding the area under the curve) gives the displacement. |
Numerical integration
-
If we had a set of numerical values for f(t) – whether experimental
values or values calculated for a given mathematical function – then we
could integrate just as described above: mutliple f by Δt and add.
That's what my pocket calculator does when I hit the "∫" key. You've
probably thought that it would be smart to space the limits of Δt on
either side of the time whose value you used to get f: that's a good
idea and you should remember it when you have to do a numerical
integration.
A very important practical point: when we made Δt small in
differentiation, we encountered the problem that the ratio Δx/Δt became
sensitive to experimental or computational error as Δt became small.
This problem does not arise in multiplication. Even better, the
computation errors, being sometimes positive and sometimes negative,
tend to cancel out. So numerical integration is much easier and safer
than numerical differentiation. The latter requires considerable caution
(and that is why my calculator doesn't have a "differentiate" button).
Analytical integration
-
This section might be shorter than you expect. We've mentioned above that integration is the opposite to differentiation:
- The integral of tm is tm+1/(m+1)
- The rate at which something changes is its derivative, but
You can recover that something by integrating the rate at which it changes. In differentiation, we subtract V(t) from V(t+dt) and divide by dt
In integration we multiply f(t) by dt and add it to V(t), where f is the derivative of V with respect to t.
-
The derivative of tn is ntn-1, so
The integral of ntn-1 is tn
The exponential function
On the graph, the curve (purple) shows e x vs x. In this the derivative is not shown in red, because the function and its derivative are equal. The straight line (green) is y = e x. At x = 1, the slope of the curve is e 1 = e . This is also the value of y at x = 1. Notice that, at x= 0, the slope of the curve is one. At x = −1, the slope is 1/e , etc. Using the chain rule tells us that
| 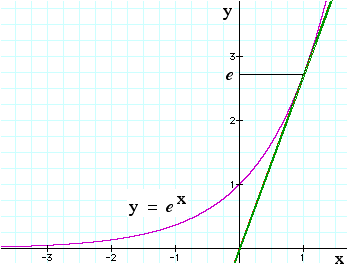 |
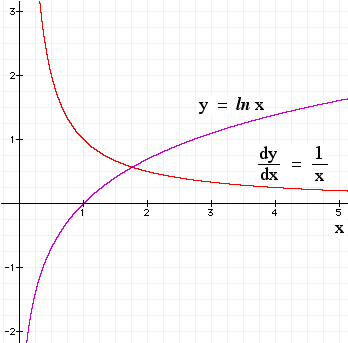
1/x and the log function
So, in the plot at right, the purple curve is y = ln x. Its slope (the rate at which it is increasing) is given by the red curve (dy/dx = 1/x). Alternatively, we could say that the purple curve rises at a rate given by the red curve (integration of a function means successively adding its value). For this and later sections, you'll notice that the examples use numbers x and y, rather than displacements as a function of time. Quantities with dimensions add extra constants, as we see below, and it is easier to begin without them. |
The integral of sine and cos
-
Above we saw that the derivative of sin θ is cos θ, and the derivative of cos θ is − sin θ. So
- The integral of cos θ is sin θ, and
- the integral of sin θ is − cos θ.
Techniques for integration
-
You need to assemble a little collection of integrals of simple
functions, including those listed immediately above. There is a range of
techniques for integrating more complicated expressions. In approximate
order of frequency, these are the techniques I use:
- Change the variables to make it more closely resemble an integral I do know. Here are a couple of examples:
- to integrate dx/(1+x), try the substitution y = 1 + x. Here dy is equal to dx, so this gives an integral we've seen above: dy/y = d ln y.
- to integrate x.dx(1 − x2)−1/2, which arises in different areas of physics, try the subsitution x = sin θ. We can now write (1 − x2) = cos θ, and dx = cos θ.dθ. Wow, that now looks much easier! (This is just one of a whole family of trigonometric substitutions.)
- Integrate by parts. This technique comes from the derivative of the product of two functions. (This is getting beyond what we need for the material here, so see a book on calculus for more details.)
- Look up a table of integrals! These have pages and pages of integrals, which are presumably assembled "the other way round" – i.e. the authors probably make a table of derivatives, then index it in terms of the integrals. Here's one on Wikipedia.
- Try an algebraic mathematical package. (Where this is useful, it often makes you feel like a dill for not having seen it yourself.)
- Integrate numerically – for many problems, this is the only way.
Komentar
Posting Komentar